Glauben Sie noch, dass sich Aufwände in der Softwareentwicklung abschätzen lassen? Ja, wirklich? Dann beruht Ihr Glaube zumindest zum Teil auf der Vorstellungen, dass sich Schätzfehler ausgleichen. Mal schätzen Sie etwas zu wenig Aufwand, ein andermal aber schätzen Sie etwas zu viel Aufwand. Oder?
Ja, das hört sich plausibel an. Manche Aufgaben stellen sich als schwieriger heraus, als gedacht, andere als leichter. In Summe heben sich also die Schätzfehler auf. Deshalb funktioniert das Schätzen unterm Strich, auch wenn es nicht fehlerfrei ist.
Ok, dann hier ein Gedankenexperiment:
Das Spiel
Sie haben eine Münze, mit der Sie Kopf oder Zahl mit einer Wahrscheinlichkeit von jeweils 0,5 werfen können.
Nun bekommen Sie das Angebot, mit dem Münzwurf Geld zu verdienen - oder zu verlieren. Wenn Sie Kopf werfen, bekommen Sie 1€, wenn Sie Zahl werfen, dann müssen Sie 1€ abgeben. Es geht also um +1€ und –1€ mit einer 50%igen Wahrscheinlichkeit.
Wenn Sie mit 0€ auf Ihrem Spielkonto beginnen würden, wie viel Geld wäre ungefähr nach 50 Würfen darauf?
a) ca. 0€ b) ein deutlich von 0€ abweichender Betrag
Überlegen Sie ruhig einen Moment…
Ich habe diese Frage einigen mathematisch normal gebildeten Menschen gestellt. Deren überwiegende Antwort war a). Sie glauben, dass sie mit so einem Spiel über 50 Würfe weder Geld verdienen noch verlieren würden.
Die Begründung: Gewinn und Verlust gleichen sich ja wegen der Wahrscheinlichkeit von 50% für beide Ergebnisse aus.
Die Statistik
Die Antwort aus dem Bauch heraus ist verständlich. Sie ist auch korrekt für eine genügend große Zahl von Spielen. Über ganz viele Spiele hinweg sollte der Kontostand bei 0€ sein. So wie der Mittelwert über viele Münzwürfe (Kontobewegungen) auch 0€ ist.
Die Frage war ja aber nicht, wie der Kontostand im Mittel am Ende von vielen Spielen wohl wäre, sondern am Ende eines Spieles. Und da liegt die Antwort aus dem Bauch heraus weit neben der Realität.
Am Ende eines Spieles ist der Kontostand sehr wahrscheinlich deutlich von 0€ abweichend. Hier als Beispiel ein Simulationsergebnis:
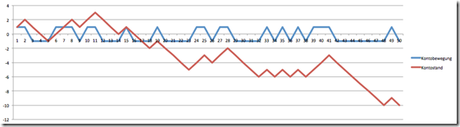
Sie sehen, am Ende des Spiels hätten Sie 10€ verloren!
Oder hier ein Verlust von 4€:
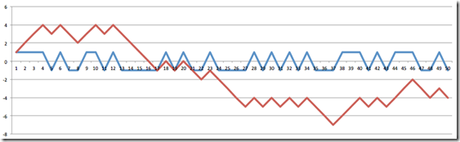
Oder hier ein Verlust von 16€:
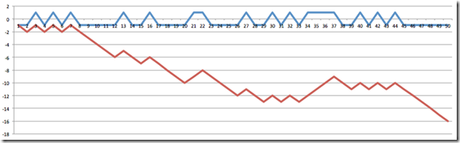
Oder hier, oh, ein Gewinn von 4€:
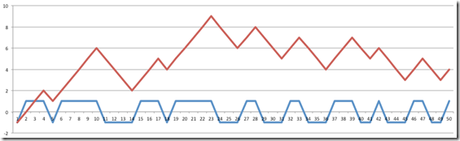
Usw. usf.
Die Kontobewegungen (blaue Linie) in den Simulationen bewegen sich hübsch pendelnd um die Nulllinie. Pro Spiel ist die Zahl der Würfe groß. Der Mittelwert der Kontobewegungen ist nahe 0€.
Doch die Kontostände… die bewegen sich deutlich unterhalb oder oberhalb der Nulllinie.
Noch ein Beispiel gefällig? Hier ein Gewinn von 5€ - allerdings nur bis knapp nach der Spielmitte. Danach stürzt das Konto ab auf –6€.
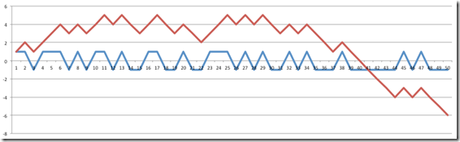
Sie sehen, auch das Spiel mit einer Wahrscheinlichkeit von 50% für Gewinn und Verlust ist ein Spiel, bei dem Sie deutlich verlieren (oder gewinnen) können.
Auf der schiefen Bahn
So weit das faire Spiel. Beide Münzseiten werden mit derselben Wahrscheinlichkeit geworfen. Was aber, wenn die Münze unregelmäßig ist? Was, wenn Sie mit etwas größerer Wahrscheinlichkeit verlieren? Statt 50% Gewinnchance haben Sie vielleicht nur 45%. Dann kann Ihnen das passieren:
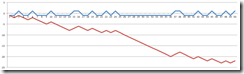
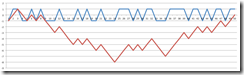
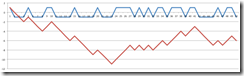
Klar, das Ergebnis muss nicht immer unter 0€ liegen - aber selbst im Mittel über viele Spiele hinweg, werden Sie die 0€ nicht mehr erreichen, sondern Verlust machen. Und das wird immer schlimmer, je weiter sich die Wahrscheinlichkeit für Zahl zu Ihren Ungunsten verschiebt.
Mit einer größeren Wahrscheinlichkeit für Verlust als für Gewinn kommen Sie auf eine schiefe Bahn. Sie rutschen in die Spielschulden. Garantiert über mehrere Spiele hinweg. Aber auch steiler innerhalb nur eines Spieles.
Geschätzte Annahmen
Nun zurück zur Softwareentwicklung. Ich denke, Sie verstehen, worauf ich mit diesem Gedankenexperiment hinaus will:
Selbst wenn sich Ihre Schätzfehler aufheben, laufen Sie Gefahr, Ihr Projekt ins Desaster zu fahren.
Ihr Projekt ist wie ein Spiel. In dem schätzen Sie 50 Aufwände oder 100 oder 500… Das bedeutet aber nicht, dass Sie bei sich aufhebenden Schätzfehlern am Ende on time, on budget herauskommen. Wie die Simulationen zeigen, können Sie sich weit, weit in die Miesen gefahren haben. Und das, obwohl die Wahrscheinlichkeit für positives und negatives Verschätzen gleich sind.
Sie könnten auch gewinnen. Das stimmt. Aber wollen Sie bei einem Projekt wirklich spielen? Ist es das, was Sie für Ihren Kunden sein wollen: ein Spieler, der auf sein Glück hofft?
Wie die Grafiken zeigen, kann Sie das Glück ganz schön pro Spiel, ich meine, pro Projekt im Stich lassen. Und das, obwohl hier sehr günstige Annahmen zugrunde liegen.
Annahme 1: Positives und negatives Verschätzen gleichen sich aus. Ist das aber in der Realität wirklich, wirklich anzunehmen? Das glaube ich nicht. Diese Abschätzung, die Sie da machen, dass das Verschätzen eine Wahrscheinlichkeit von 50:50 hat, hat einen Fehler. So wie ich die Entwicklungsrealität kennengelernt habe, verschätzen Sie sich mit viel größerer Wahrscheinlichkeit zu Ihren Ungunsten. Wir müssten also nicht mit 50:50 simulieren, sondern eher mit 20:80: nur mit einer Wahrscheinlichkeit von 0,2 schätzen Sie zu große Aufwände; in 80% der Fälle schätzen Sie jedoch zu kleine Aufwände. Damit fährt das “Projektkonto” direkt in die Miesen. Probieren Sie es selbst aus in einer kleinen Excel-Simulation.
Annahme 2: Wenn Sie glauben, dass Sie sich in etwas so oft zu Ihren Gunsten wie zu Ihren Ungunsten verschätzen, dann beziehen Sie das wahrscheinlich auf die Anzahl Ihrer Schätzungen: bei 50 Schätzungen schätzen Sie 25 Mal zu wenig und 25 Mal zu viel.
Aber was ist eigentlich mit der Größe des geschätzten Aufwandes? Der hängt von der Größe der Aufgabe ab. Diese Größe variiert jedoch wahrscheinlich beträchtlich. Mal sind die Aufgaben klein, mal sind sie größer, dann sogar groß. Wie ist diese Größenverteilung? Und verschätzen Sie sich bei jeder Größe in gleicher Weise?
Glauben Sie wirklich, dass Sie auch das realistisch einschätzen? Ich erlaube mir, das zu bezweifeln.
Wenn nun aber die Größen der Aufgaben unterschiedlich sind und Ihr Schätzfehler ebenfalls unterschiedlich ist… dann wird damit die Unvorhersehbarkeit des “Projektspiels” angeheizt.
TL;DR
Wenn Sie glauben, Aufwandsschätzungen in der Softwareentwicklung könnten funktionieren, weil sich positive und negative Schätzfehler doch aufheben würden… dann machen Sie die Softwareentwicklung zu einem Glücksspiel. Denn auch bei 50:50 Chancen für Gewinn und Verlust, kann Sie ein einziges Spiel mit mehreren “Würfen” weit in die Miesen führen.
Dafür, dass das Gesetz der großen Zahl Ihnen ein ausgeglichenes Konto beschert, führen Sie einfach zu wenige Projekte durch.
Widerstehen Sie also der Spielsucht. Glauben Sie nicht länger, am Ende doch noch abzuräumen und alle Schulden zurückzuzahlen.


