Parabeln lernen quadratische Gleichungen

Parabeln für Gönke

Ich kann

• Scheitelpunkt ausrechnen :(  :/  :)
• Nullstellen mit Scheitelpunktform
• Nullstellen mit pq Formel
• Wertetabelle aufstellen
• Zeichnen der Parabel von Wertetabelle
• Zeichnen der Parabel durch Scheitelpunktform
• Zuordnen von Parabeln die gezeichnet sind mit Beispielaufgaben ( Realschulprüfung )
• Schnittpunkt m y Achse ablesen
• Ablesen ob sie nach oben oder nach unten geöffnet ist
• Ablesen ob sie gestreckt oder gestaucht ist
• Ablesen wohin sie verschoben ist
• Erstmal ausmulitplizieren
• Umwandel von der Scheitelpunktform in die Normalenform
• aus einer Zeichnung die Funktionsgleichung errechnen
• aus Punkten die Funktionsgleichung errechnen
• Schnittpunkt mit einer anderen Funktion
• Satz von Vieta

Inhalt

• Begriffe
• Wie Parabeln aussehen können
• Nullstellen ausrechnen mit der quadratischen Ergänzung
• Nullstellen ausrechnen mit der pq Formel
• Scheitelpunkt berechnen mit der quadratischen Ergänzung
• Wertetabelle herstellen
• Ordinatenschnittpunkt ablesen ( Schnittpunkt mit der y Achse )

Begriffe

• Scheitelpunkt: Der Scheitelpunkt ist der höchste oder der tiefste Punkt des Grafen ( bei einer positven Parabel - eine die lacht der tiefste Punkt). Bei einer umgedrehten Parabel ( x² ist negativ ) ist es der höchste Punkt.
• Nullstellen- hier schneidet die Parabel die x Achse
• Ordinatenschnittpunkt - der Graph der Parabel schneidet die y Achse

Was man schon aus der Funktionsgleichung erkennen kann ( in der Normalenform)

das x² kann uns schon viel verraten
Ist das x² postitiv so ist die Parabel nach oben geöffnet ( lacht )
Ist das x² negativ so ist die Parabel nach unten offen ( ist traurig )

der Faktor ohne x verrät uns, wo die Parabel die y Achse schneidet

Die Funktionsgleichung in der Scheitelpunktform macht es uns möglich einfach den Scheitelpunkt abzulesen

Verschiedene Gleichungen der  Funktionen
Es gibt einmal die ganz normale Form, die nennt man Polynomform
allgemein schreibst du die so
y=ax²+bx+c
y=x²+2x+3
Die Scheitelpunktform
die sieht allgemein so aus
y=a( x+u)²+v
U ist der umgedrehte x Wert vom Scheitelpunkt und v der y Wert
y=(x-3)²+2
und dann noch eine wo man die Nullstellen direkt ablesen kann
allgemein nennt man das die Linearfaktorschreibweise
y=a(x-x1)(x-x2)
y=-(x+3)(x-4)
Die Nullstellen sind -3 und +4

Wertetabelle-->sillebehn :D

Warum macht man eine Wertetabelle

Man macht eine Wertetabelle, um die Funktion zeichnerisch darstellen zu können und um schon eine Vorstellung von den wichtigen Punkten zu bekommen. Vieles kann man aus der Wertetabelle ablesen.

Wie macht man eine Wertetabelle

Wenn man die Funktionsgleichung hat, dann verwendet man sie wie eine Formel: Man setzt einen x Wert ein und bekommt einen y Wert. Man rechnet jeden Punkt einzelnd aus.

y=2x²-2x+1

-2 -1 0 1 2

Ergebnis135115

Rechnung2*-2²-2*-2+12*-1²-2*-1+12*-0²-2*-0+12*1²-2*1+12*2²-2*2+1

Du kannst die Wertetabelle auch mit Deinem Taschenrechner machen:
Man gibt beim Casio ein : Mode und wählt dann Table aus. Danach gibst Du die Funktionsgleichung ein, für x schreibst Du auch x! Das findest Du durch die Tastenkombination Alpha und ). Danach gibst Du an wo die Tabelle starten soll( hier -2) und wo sie endet ( 2 ) immer von Minus nach Plus. Step , die Schrittweite wird auch abgefragt, hier nehmen wir 1! Bestätigt wird immer mit =. Danach kannst du die Tabelle einfach ablesen.

Was man aus der Wertetabelle rauslesen kann.
Scheitelpunkt
Wenn wir eine postive Funktion haben ( eine lachende), dann werden die Werte erstmal kleiner und immer kleiner. Irgendwann werden sie wieder größer in der Wertetablle. Hier ist das der Fall nach X=0 und x=1, bis 0 werden die immer kleiner, danach wachsen die wieder an. Also liegt unser Scheitelpunkt genau da, wo die Werte am niedrigsten sind .

Bei einer negativen Parabel ( also eine nach unten geöffnete, traurige),ist es genau umgekehrt. Die Werte werden ersteinmal größer und immer größer. Irgendwann haben sie den Höhepunkt erreicht und werden wieder kleiner. Das kann man aus der Wertetabelle ersehen.

Den Scheitelpunkt kann man von der Scheitelpunktform ablesen, diese erhält man, wenn man die quadratische Ergänzung anwendet.

Nullstellen

Wenn wir oben einen Wert für x haben und im unteren Kästchen eine Null, dann haben wir eine Nullstelle gefunden. Dies ist bei x=0 und x=1 der Fall.

Die Nullstellen kann man ausrechnen, indem man die pq Formel anwendet oder indem man die Scheitelpunktform umformt.

Vorarbeit
Quadratische Ergänzung
Wenn ich Euch im Folgenden beauftrage die quadratische Ergänzung zu verwenden, dann macht ihr erstmal x² zum Single. Danach nehmt ihr das mit x ( nicht das mit x²)
1. nehmt das x weg
2. teilt die Zahl durch 2
3. nehmt die Zahl zum Quadrat ( also mit sich selbst mal )
4.hängt die Zahl einmal mit +und einmal mit - dahinter

Nullstellen ausrechnen
mit der quadratischen Ergänzung

1. Ihr habt die Funktionsgleichung in der normalen Form. Jetzt muss x² alleine stehen, ihr teilt also alles durch den Faktor vor x².
2. Im nächsten Schritt wendet Ihr die quadratische Ergänzung an. Das mit dem x durch 2 teilen, vorher das x entfernen, dann quadrieren und einmal mit +und einmal mit Minus hinter den Term
3. Anschließend sortiert ihr das so: x²  das mit x quadratische Ergänzung mit Plus das mit nix, quadratische Ergänzung mit Minus
4. Jetzt fasst Ihr die ersten Drei zu einem der drei Binome zusammen ( eigentlich sind es immer die ersten beiden Binome ), Wurzel aus x vorne in die Klammer, das Vorzeichen vom Term mit x in die Klammer und denn die Wurzel aus der positvien quadratischen Ergänzung in die Klammer,Klammer zu quadrat dahinter
5. Jetzt müsst ihr nur noch die  beiden übrig gebliebenen Faktoren zusammenrechnen ( also das mit x und die negative quadratische Ergänzung)
6. Das was nicht im Binom steht holt ihr dann auf die andere Seite
7. Jetzt zieht ihr aus allem die Wurzel ( auf der einen Seite steht dann x und Zahl , auf der anderen eine Zahl. War das auf der anderen Seite negativ kann man keine Wurzel ziehen, dann gibt es keine Nullstellen . Könnt ihr die Wurzel ziehen dann ist die Zahl rechts einmal positiv und einmal negativ ( wir haben ja zwei Nullstellen )
8. Jetzt die Zahl beim x noch rüberziehen zu der Zahl auf der rechten Seite, einmal zum positiven TEil und dann noch einmal zum  negativen Teil.
9. Fertig

Beispiel

1. y=x²+6x-7  steht für sich allein, hier müssen wir nix machen
2. 6x durch 2 und hoch zwei sind +9  und -9, also  x²+6x-7+9-9=0
3. sortieren x²+6x+9-7-9
4. Binom (x+3)²--7-9=0
5. (x+3)²-16=0
6. (x+3)²=16 rüberziehen
7. Wurzel x+3=4(+und -)
8. drei rüberziehen x=+4-3= 1  und x=-4-3=-7

mit der pq Formel

Die pq Formel ist eigentlich überflüssig, wenn man die quadratische Ergänzung hat, die man umstellen kann. Aber viele Lehrer fragen genau hiernach.

Die Formel ist: Minus p halbe, plus minus die Wurzel aus ( Phalbe²-q)

Zwei Merksätze gelten: x² muss Single sein ( also davor darf nix stehen )
und ihr erkennt das p am x das q am nix

Wenn ihr euch das einfach machen wollt, dann rechnet ihr die Teile von der Formel  schon mal vorab aus, damit ihr das beim rechnen leichter habt.
Bei dem mit nix, dem q, dreht ihr das Vorzeichen einfach um
p halbiert ihr schon mal
und dann quadriert ihr das noch mal (na fällt euch was auf?? Durch zwei hoch zwei, genau:Quadratische Ergänzung, aber das nur mal so by the way)

Beispiel

y=x²+6x-7
Hier steht nix vorm x² das ist schon mal gut.
Jetzt bestimmen wir:p mit x ist also 6 und q mit nix, ist also -7
denkt immer dran die Vorzeichen mitzunehmen
weil ich es gern einfach habe mache ich immer folgende Aufstellung
p=6
Phable=3
Phalbe²=9
-Phalbe=-3
q=-7
-q ist 7

Jetzt muss ich das nur noch in die Formel eintragen: -3 +-Wurzel aus (9+7)
also -3+Wurzel aus 16= -3+4 sind 1
und -3-Wurzel aus 16 sind -3-4 sind -7

fertig
Beim q müsst ihr immer das Vorzeichen umdrehen. Das ist die häufigste Fehlerquelle

Nullstellen mit dem Taschenrechner ausrechnen:

Zwei Möglichkeiten habt Ihr, um die Nullstellen mit dem Taschenrechner auszurechnen. Die eine ist die schnelle Möglichkeit, bei der Euch aber nur eine Lösung angezeigt wird. Die könnnt ihr auch immer anwenden, wenn ihr einfache Gleichungen lösen müsst
erst die Funktion mit x eingeben und dann drückt ihr Shift und Calc ( also Solve),der fragt dann ob ihr nach x solven sollt und das bestätigt ihr dann
y=x²+6x-7
Ihr gebt nur das hier ein  x²+6x-7 und dann Shift und Calc herauskommt 1,05

Der zweite Weg führt über Mode - EQN und dann müsst ihr den Punkt ax²+bx+c=0 wählen( der sieht ja auch wie unsere Parabeln aus ). Jetzt die Zahlen eingeben ohne die xe, aber mit den Vorzeichen
also 1, dann 6 dann -7 immer bestätigen mit = heraus kommt x1=1 und x2=-7 also beide Nullstellen.

Scheitelpunkt ausrechnen ( wie Nullstellen mit der quadratischen Ergänzung - same shit but different :D)
Es ist bis Punkt Fünf exakt das selbe. Kopiere es noch mal hier rein, damit ihr ne komplette Erklärung habt

1. Ihr habt die Funktionsgleichung in der normalen Form. Jetzt muss x² alleine stehen, ihr teilt also alles durch den Faktor vor x².
2. Im nächsten Schritt wendet Ihr die quadratische Ergänzung an. Das mit dem x durch 2 teilen, vorher das x entfernen, dann quadrieren und einmal mit +und einmal mit Minus hinter den Term
3. Anschließend sortiert ihr das so: x²  das mit x quadratische Ergänzung mit Plus das mit nix, quadratische Ergänzung mit Minus
4. Jetzt fasst Ihr die ersten Drei zu einem der drei Binome zusammen ( eigentlich sind es immer die ersten beiden Binome ), Wurzel aus x vorne in die Klammer, das Vorzeichen vom Term mit x in die Klammer und denn die Wurzel aus der positvien quadratischen Ergänzung in die Klammer,Klammer zu quadrat dahinter
5. Jetzt müsst ihr nur noch die  beiden übrig gebliebenen Faktoren zusammenrechnen ( also das mit x und die negative quadratische Ergänzung)
6. Das in der Klammer ist jetzt unsere x Koordinate vom Scheitelpunkt. Diese gilt aber nur, wenn ihr das Vorzeichen umdreht. Die Sachen ohne x ausserhalb der Klammer sind die y  Werte unseres Scheitelpunkt

1. y=x²+6x-7 steht für sich allein, hier müssen wir nix machen
2. 6x durch 2 und hoch zwei sind +9  und -9, also  x²+6x-7+9-9=0
3. sortieren x²+6x+9-7-9
4. Binom (x+3)²--7-9=0
5. (x+3)²-16=0
6. Scheitelpunkt (-3/-16)

Schnittpunkt zwischen einer linearen Funktion ( Gerade ) und einer Parabel ausrechnen bzw einer Parabel
Das ist bei beiden eigentlich das selbe.

Diese Schritte müsst Ihr machen:

1. Gleichungen gleichsetzen
2. alles auf eine Seite packen
3. Lösungsmenge bestimmen (zB mit PQ Formel )

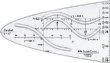
Beispiel
Bestimmen Sie den Schnittpunkt zwischen f(x)=x² und g(x)=x+ 3/4 ( dreiviertel)
gleichsetzen  x²=x+3/4
auf eine Seite bringen  x²-x-3/4
dann Lösungsmenge bestimmen
p=-1  phalbe=- 1/2 phalbe²=1/4
minus q ist3/4
also
1/2 plus die Wurzel aus 1/4 plus 3/4 
1/2 minus die Wurzel aus 1/4 plus 3/4
=1/2 plus 1= 1,5
und
=1/2-1=-0,5

Wenn die Gleichungen noch nicht so schön ausgeformt sind, dann müsst ihr die Klammern erstmal ausmulitplizieren

Hier als Beispiel Nummer 5a
x(x-6)+8=7-4(x-1)
Jetzt müssen wir die Klammern ausmultiplizieren
x²-6x+8=7-4x+4
Jetzt x zu x nix zu nix
x²-6x+8=-4x+11
Jetzt alles rüberholen
x²-6x+8+4x-11=0
Jetzt wieder zusammenfassen
x²-2x-2=0
hier geht es dann ganz normal weiter

Wenn wir (  )² haben, dann schreiben wir die Klammern noch einmal nebeneinander hin und mulitplizieren sie dann aus, es sind nämlich BINOME (siehe unten )
Beispielaufgabe 6f
(4x-5)²-(3x-4)²=(x-5)²+20
(4x-5)(4x-5)-(3x-4)(3x-4)=(x-5)(x-5)+20
14x²-20x-20x+25-(9x²-12x-12x+16)=x²-5x-5x+25+20
Das Minus vor dem zweiten Binom ändert die Vorzeichen in der Klammer ausserdem fassen wir jetzt schon mal etwas zusammen
14x²-40x+25-9x²+24x-16=x²-10x+45

fassen wir jetzt zusammen
5x²-16x+9=x²-10x+45

Wiederholungswissen aus den Klassen vorher

Binome
1. (a+b)²= a²+2ab+b²
2. (a-b)²= a²-2ab+b²
3. (a+b)(a-b)= a²-b²
Dänenspezial

y=x²+6x-7

-2-1012

Ergebnis-15-12-709

Und so rechnen die Dänen das:D Das nennt man auch Diskriminantenverfahren glaub ich

Die Funktion sieht so aus y=ax²+bx+c
Die Zahlen übernehmen wir y=x²+6x-7
a=1
b=+6
c=-7
Jetzt rechnen wir die Diskriminant (e) aus

D= b²-4ac
D=6²-4*1*-7
D=64

Die Sillebeen ( Wertetabelle)

y=x²+6x-7

-2-1012

Ergebnis-15-12-709

Toppunkt ( Scheitelpunkt )
x Koordinate
-b/2a
-6/2
also -3
y Koordinate
-D / 4a
-64/4
-16
Also S ( -3/-16)

Die Lösning entspricht den Nullstellen
x= -b +- Wurzel aus (D) DURCH 2a
also
x=
-6 + Wurzel aus 64 / 2*1
(-6 +8)/2=  1
und die andere
-6 -Wurzel aus 64 / 2*1
(-6 -8)/2= -7

Übungen für Gönke und Sarah und Niklas
Nullstellen bestimmen ( auf beide Arten),Scheitelpunkt und Wertetabelle, zeichnen, und die Schnittpunkte mit der y Achse bestimmen
x²+2x+2
x²+2x-2
3 x²-x+4
3x²+3x-1
2(x-2)²-2
x²-2x+3
2x²+3x-2
-3x²+2x+1
Videos

http://youtu.be/pMDPzgPWtKY
http://youtu.be/pMDPzgPWtKY
http://youtu.be/oTiQLxvqYgc
http://youtu.be/FB27E49jEv0
http://youtu.be/SjfqxiE-w1o
http://youtu.be/0ciHpxe0t2k
http://youtu.be/jALYnfNuOvc
http://youtu.be/GzXUj8YvZT4
http://youtu.be/mRG9UGSQy8o

Erklärungen

http://nibis.ni.schule.de/~lbs-gym/klasse9pdf/Parabeln.pdf
http://miami.uni-muenster.de/servlets/DerivateServlet/Derivate-3157/Stachniss_Stationen_vers2_240804.pdf
http://www.re-wi.de/MathDiff.pdf

Übungen

http://www.realmath.de/Neues/Klasse9/parabueb/liegtqaufp.html
http://www.realmath.de/Neues/Klasse9/parabueb/koordrechnen.html
http://www.realmath.de/Neues/Klasse9/parabueb/koordrechnen02.html
http://www.realmath.de/Neues/Klasse9/parabueb/koordrechnen03.html
http://www.realmath.de/Neues/Klasse9/parabueb/basketball.html
http://www.realmath.de/Neues/Klasse9/parabueb/parabelortslinie.html
http://www.realmath.de/Neues/Klasse9/wurzel/wurzelfunktion.php
http://www.realmath.de/Neues/Klasse9/parabueb/parabelzeichnen1.html
http://www.realmath.de/Neues/Klasse9/parabueb/parabelzeichnen2.html
http://www.realmath.de/Neues/Klasse9/parabueb/parabelzeichnen01.html
http://www.realmath.de/Neues/Klasse9/parabueb/parabelquiz.html
http://www.realmath.de/Neues/Klasse9/parabueb/parabelquiz2.html
http://www.realmath.de/Neues/Klasse9/parabueb/parabelscheitel01.html
http://www.realmath.de/Neues/Klasse9/parabueb/pqscheitel.html
http://www.realmath.de/Neues/Klasse9/parabueb/pqscheitelueb.html
http://www.realmath.de/Neues/Klasse9/parabueb/beispextrem1.html
http://www.realmath.de/Neues/Klasse9/Parabel/parabel.php
http://www.realmath.de/Neues/Klasse9/Parabel/parabelvektor.php
http://www.realmath.de/Neues/Klasse9/Parabel/scheitelform.php
http://www.realmath.de/Neues/Klasse9/parabueb/parabelscheitel.html
http://www.realmath.de/Neues/Klasse9/parabueb/abcscheitel.html
http://www.realmath.de/Neues/Klasse9/parabueb/allgscheitel.html
http://www.realmath.de/Neues/Klasse9/parabueb/parabelzeichnen.html
http://www.realmath.de/Neues/Klasse9/parabueb/profiparabel.html
http://www.realmath.de/Neues/Klasse9/parabueb/parabelablesen.html
http://www.realmath.de/Neues/Klasse9/Parabel/tabelleundgraf.html
http://www.realmath.de/Neues/Klasse9/Parabel/pqparabel.html